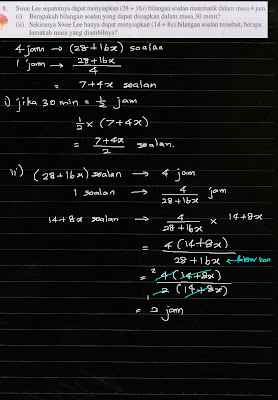cikguazmanbukitjalil.blogspot.com

F4 Math Praktis Kendiri 1.1e Q3-4 Bab 1 Fungsi dan Persamaan Kuadratik Praktis Kendiri 1.1e Q3-4 Soalan 3 dan 4 3. Bagi setiap yang berikut, tentukan sama ada setiap nilai berikut merupakan punca bagi persamaan kuadratik yang diberikan. (a) (x – 1)(x + 4) = 0; x = – 4, x = 2, x = 1 (b) 2(x – 3)(x – 5) = 0; x = –3, x = 3, x = 5 (c) 3(2 + x)(x – 4) = 0; x = –2, x = 2, x = 4 4. Bagi graf fungsi kuadratik di sebelah, tentukan sama ada nilai x yang diberikan merupakan punca bagi persamaan kuadratik f (x) = 0. (a) x = 1 (b) x = –3 (c) x = 15 (d) x = 5

F4 Math Praktis Kendiri 1.1e Q1-2 Bab 1 Fungsi dan Persamaan Kuadratik Praktis Kendiri 1.1e Soalan 1 dan 2 1. Bagi setiap graf fungsi kuadratik di bawah, nyatakan punca-punca bagi persamaan kuadratik yang diberikan. (a) 3x2 – 5x – 2 = 0 (b) –x2 + x + 20 = 0 2. Bagi setiap yang berikut, tentukan sama ada setiap nilai berikut merupakan punca bagi persamaan kuadratik yang diberikan atau bukan. (a) x2 – 5x + 6 = 0; x = 3, x = 2  (b) 2x2 – x – 1 = 0; x = 1, x = 1/2 (c) 3x2 – 5x – 2 = 0; x = – 1/3, x = –2  (d) 3x2 + 4x + 2 = 6; x = 2, x = 2/3

F4 Addmath Bab 1 Fungsi Q5 Latih Diri 1.7 Q5 Latih Diri 1.7 Soalan 5 5. Seketul batu kecil dibaling ke dalam sebuah kolam yang tenang dan menghasilkan riak air berbentuk bulatan. Jejari, r, dalam cm, bagi riak air itu bertambah dengan kadar 3 cm per saat. (a) Cari ungkapan bagi jejari, r, dalam sebutan masa, t, selepas batu itu dibaling. (b) Jika A ialah luas riak air, terangkan maksud fungsi gubahan Ar(t). (c) Cari luas A, riak air itu selepas 30 saat.

Bab 2 Pemfaktoran dan Pecahan Algebra Q5 Menjana Kecemerlangan Menjana Kecemerlangan Soalan 5

Bab 2 Pemfaktoran dan Pecahan Algebra Q6 Menjana Kecemerlangan  Menjana Kecemerlangan Soalan 6

Bab 2 Pemfaktoran dan Pecahan Algebra Q7 Menjana Kecemerlangan  Menjana Kecemerlangan Soalan 7 Soalan 8

Bab 2 Pemfaktoran dan Pecahan Algebra Q8 Menjana Kecemerlangan Menjana Kecemerlangan Soalan 8 Soalan 9

Bab 2 Pemfaktoran dan Pecahan Algebra Q9 Menjana Kecemerlangan Menjana Kecemerlangan Soalan 9 Soalan 10

Bab 2 Pemfaktoran dan Pecahan Algebra Q10 Menjana Kecemerlangan Menjana Kecemerlangan Soalan 10

F4 AddMath Bab 1 Fungsi Songsang Latih Diri 1.10 Q5 Latih Diri 1.10 Q5 Soalan 5 5. Fungsi songsang g–1 ditakrifkan oleh g–1 : x → 4 2 – x, x ≠ k. (a) Nyatakan nilai k. (b) Cari g(12 ).

F5 Addmath Latihan Formatif 3.4 Q2 Bab 3 PENGAMIRAN Latihan Formatif 3.4 Q2 Soalan 2 Rajah di sebelah menunjukkan keratan rentas sebuah penutup mesin yang dihasilkan oleh mesin pencetak 3D. Penutup itu diperbuat daripada sejenis bahan pencetak, iaitu filamen plastik. Bahagian dalam dan bahagian luar penutup itu masing-masing boleh diwakili oleh y = – 1 16 x 2 + 2.8 dan y = – 1 20 x 2 + 3. Anggarkan kos, dalam RM, filamen plastik yang digunakan untuk menghasilkan 20 penutup yang sama jika harga 1 cm3 filamen plastik ialah 7 sen.

F5 Addmath Latihan Formatif 3.4 Q1 Bab 3 PENGAMIRAN Latihan Formatif 3.4 Q1 Soalan 1 Sebuah kilang menghasilkan minyak masak sawit. Didapati bahawa sebuah tangki minyak yang berbentuk silinder di kilang tersebut mengalami kebocoran. Tinggi minyak dalam tangki itu berkurang dengan kadar 5 cmmin –1 dan kadar perubahan isi padu minyak dalam tangki terhadap tinggi minyak diberi oleh dV dh = 35 t – 6, dengan keadaan t ialah masa, dalam minit. Cari isi padu, dalam cm3, minyak yang mengalir keluar daripada tangki itu selepas 0.5 jam.

F5 Addmath Latihan Sumatif Q16 Bab 2 Pembezaan Latihan Sumatif Q16 Soalan 16 Rajah di sebelah menunjukkan sebuah bekas berbentuk kon terbalik dengan jejari 12 cm dan tinggi 20 cm. TP 6 (a) Jika tinggi air di dalam bekas itu ialah h cm, tunjukkan bahawa isi padu air, V cm3, di dalam bekas itu diberi oleh V = 3 25 π h3. (b) Air mengalir keluar melalui lubang di hujung bekas, (i) cari perubahan kecil dalam isi padu air apabila h menyusut daripada 5 cm kepada 4.99 cm, (ii) tunjukkan bahawa susutan kecil sebanyak p% dalam tinggi air itu akan menyebabkan susutan sebanyak 3p% dalam isi padu.

Bab 4 Poligon Matematik Tingkatan 2 Q9 Menjana Kecemerlangan Q9 Menjana Kecemerlangan Soalan 9 9. Berdasarkan rajah di bawah, ABCDEFGH ialah sebuah oktagon sekata dan EFKLM ialah sebuah pentagon sekata. Hitung ∠CBM.

Bab 4 Poligon Matematik Tingkatan 2 Q8 Menjana Kecemerlangan Q8 Menjana Kecemerlangan Soalan 8

Bab 4 Poligon Matematik Tingkatan 2 Q4-5 Menjana Kecemerlangan Q4-5 Menjana Kecemerlangan Soalan 4 Soalan 4 dan 5

Bab 4 Poligon Matematik Tingkatan 2 Q3 Menjana Kecemerlangan Q3 Menjana Kecemerlangan Soalan 3

F5 Addmath Latihan Kendiri 6.9 Q4 Bab 6 FUNGSI TRIGONOMETRI Latihan Kendiri 6.9 Q4 Soalan 4 4. Diberi sin x = 45 dengan x ialah sudut tirus dan sin y = 5 13 dengan y ialah sudut cakah, cari (a) kosek 2x (b) sek 2y (c) sin x2 (d) tan y2

F5 Addmath Latihan Kendiri 6.9 Q3(c)(d) Bab 6 FUNGSI TRIGONOMETRI Latihan Kendiri 6.9 Q3(c)(d) Soalan 3(c)(d) 3. Buktikan setiap identiti yang berikut. (a) sin 2q (tan q + kot q) = 2 (b) sin 4x + sin 2x kos 4x + kos 2x + 1 = tan 2x (c) kosek 2A + kot 2A = kot A (d) sek 2x = kot x + tan x kot x – tan x

F5 Addmath Latihan Kendiri 6.9 Q3(a)(b) Bab 6 FUNGSI TRIGONOMETRI Latihan Kendiri 6.9 Q3(a)(b) Soalan 3(a)(b)

F4 Matematik praktis komprehensif Q12 bab 2 Asas Nombor praktis komprehensif Q12 Soalan 12 12. Azizan membeli sebuah beg yang mengandungi 100 biji bola kecil untuk anaknya. 15 daripada bola tersebut berwarna hijau, 14 berwarna kuning, 1 10 berwarna merah jambu dan yang bakinya berwarna biru. Berapakah bilangan bola berwarna biru dalam asas lapan? Soalan 1-3 klik sini Soalan 9 klik sini Soalan11 klik sini Soalan 12 Soalan 13

F5 Addmath Latihan Kendiri 6.9 Q2 Bab 6 FUNGSI TRIGONOMETRI Latihan Kendiri 6.9 Q2 Soalan 2 2. Buktikan bahawa kosek 2A = 12 sek A kosek A.

F3 Math Mahir Diri Q1 Bab 1 Indeks Mahir Diri Q1 Soalan 1 1. Ringkaskan setiap yang berikut. (a) (mn4)3 ÷ m4n5 (b) 3x × —1 y4 × (xy)3 (c) √xy × 3√xy2 × 6√xy5 Soalan Seterusnya, klik (Mahir Diri) merah di bawah untuk list menu.

F4 Addmath Bab 1 Fungsi Q3 Latih Diri 1.7 Latih Diri 1.7 Soalan 3 3. Luas permukaan sebuah belon udara panas, A, dalam m2, yang berisi udara panas diberi oleh fungsi A(r) = 4πr2 dengan r ialah jejari belon, dalam meter. Jejari belon itu bertambah sebagai fungsi masa, t, dalam saat, mengikut rumus r(t) = 23 t³, t  0. (a) Nyatakan luas permukaan belon, A, sebagai fungsi masa, t. (b) Cari luas permukaan belon setelah 2 saat. Soalan 4 4. air. Air diisi ke dalam bekas itu dengan kadar malar 100 cm3 per saat. (a) Tuliskan rumus untuk (i) kuantiti air, v, di dalam bekas itu selepas t saat, (ii) tinggi air, h, di dalam bekas itu dalam sebutan v, (iii) fungsi gubahan hv(t). (b) Cari tinggi air di dalam bekas itu selepas 20 saat.  

F4 Addmath Bab 3 Sistem Persamaan kaedah penghapusan Latihan Intensif 3.1 Latihan Intensif 3.1 Q2e-f Soalan 2e dan 2f 2. Selesaikan setiap persamaan berikut dengan kaedah penghapusan dan penggantian. (a) x + y + z = 3 (b) 2x + y – z = 7 (c) x + y + z = 3 x + z = 2 x – y + z = 2 2x + y – z = 6 2x + y + z = 5 x + y – 3z = 2 x + 2y + 3z = 2 (d) 2x – y + z = 6 (e) x + y + 2z = 4 (f) x + 2y + z = 4 3x + y – z = 2 x + y + 3z = 5 x – y + z = 1 x + 2y – 4z = 8 2x + y + z = 2 2x + y + 2z = 2

F3 Masteri Kendiri Q7 Bab 1 Indeks Masteri Kendiri Q7

F4 AddMath Bab 1 Fungsi  Latihan  Pengukuhan Q5 Latihan  Pengukuhan Q5 Soalan 5 5. Gambar rajah anak panah di sebelah mewakili sebahagian daripada pemetaan f : x → hx + kx , x ≠ 0, cari TP3 (a) nilai h dan nilai k, (b) imej bagi 6 di bawah pemetaan ini.

F4 AddMath Bab 1 Fungsi NILAI MUTLAK Latihan  Pengukuhan Q4 Latihan  Pengukuhan Soalan 4 4. Suatu fungsi f ditakrifkan oleh f : x → |x – 3| untuk domain –1  x  7. TP3 (a) Lakarkan graf f dan nyatakan julat bagi f. (b) Cari julat nilai x dengan keadaan f (x)  2. (c) Pada graf yang sama di (a), lakarkan graf y = 2x – 3 dan seterusnya dapatkan nilai x dengan keadaan |x – 3| = 2x – 3. Soalan Seterusnya, klik (Latihan  Pengukuhan) merah di bawah untuk list menu.

F5 Addmath Latihan Sumatif Q15 Bab 2 Pembezaan Latihan Sumatif Q15 Soalan 15 15. Rajah di sebelah menunjukkan sebahagian daripada lengkung y = 6x – x 2 yang melalui asalan dan titik P(x, y). TP 3 (a) Jika Q ialah titik (x, 0), tunjukkan bahawa luas, A bagi segi tiga POQ diberi oleh A = 12 (6x 2 – x 3). (b) Diberi bahawa x menokok dengan kadar 2 unit per saat, cari (i) kadar tokokan bagi A apabila x = 2, (ii) kadar susutan bagi A apabila x = 5.

F5 Addmath Latihan Sumatif Q14 Bab 2 Pembezaan Latihan Sumatif Q14 Soalan 14 14. Sebuah kubus mengembang dengan keadaan sisi-sisinya berubah pada kadar 2 cms–1. Cari kadar perubahan jumlah luas permukaan kubus itu apabila isi padunya ialah 8 cm3. 

F5 Addmath Latihan Sumatif Q13 Bab 2 Pembezaan Latihan Sumatif Q13 Soalan 13 13. Dalam rajah di sebelah, Mukhriz mendayung sebuah kayak dari titik A yang berada 30 m jauhnya dari titik terdekat B di tepi pantai lurus BD ke titik C yang berada x m dari titik B. Kemudian, dia berbasikal dari titik C ke titik D yang jauhnya 400 m dari titik B dalam masa terpantas yang mungkin. Cari jarak dari B ke C, jika dia mendayung pada halaju 40 mmin–1 dan berbasikal pada halaju 50 mmin–1.

F4 Math Praktis Kendiri 2.1b Q5 Bab 2 Asas Nombor Praktis Kendiri 2.1b Q5 Soalan 5 5. Tukar setiap nombor berikut kepada nombor dalam asas dua. (a) 438 (b) 1128 (c) 578 (d) 12178 (e) 6358 (f) 2438

F4 Math Praktis Kendiri 2.1b Q3-4 Bab 2 Asas Nombor Praktis Kendiri 2.1b Q3-4 Soalan 3 dan 4 3. Tukar nilai digit 5 dalam nombor 1546 kepada nombor dalam asas 3. 4. Tukar setiap nombor berikut kepada nombor dalam asas lapan. (a) 1111012 (b) 11102 (c) 111101112 (d) 1010102 (e) 1110002 (f) 1110101012

F5 Addmath Latihan Kendiri 3.6 Q3 Bab 3 PENGAMIRAN luas Latihan Kendiri 3.6 Q3 Soalan 3 3. (a) Jika lengkung y = –x 3 – x 2 menyilang lengkung y = –x – x 2 pada titik (–1, 0), (0, 0) dan (1, –2), cari luas rantau di antara dua lengkung itu. (b) Diberi bahawa lengkung y = x 2 – 4x dan y = 2x – x 2 bersilang pada dua titik. Cari luas bagi rantau di antara dua lengkung itu.

F5 Addmath Latihan Kendiri 3.5 Q4 Bab 3 PENGAMIRAN tentu Latihan Kendiri 3.5 Q4 Soalan 4 4. Diberi ∫ 7 3 f (x) dx = 5 dan ∫ 7 3 k(x) dx = 7. Cari nilai bagi setiap yang berikut. (a) ∫ 7 3 [f (x) + k(x)] dx (b) ∫ 5 3 f (x) dx – ∫ 5 7 f (x) dx (c) ∫ 7 3 [ f (x) + 2x] dx

F5 Addmath Latihan Kendiri 3.5 Q3 Bab 3 PENGAMIRAN tentu Latihan Kendiri 3.5 Q3 Soalan 3

F5 Addmath Latihan Formatif 3.5 Q2 Bab 3 PENGAMIRAN tentu Latihan Formatif 3.5 Q2 Soalan 2 2. Cari nilai bagi setiap kamiran tentu yang berikut. (a) ∫ 4 2 (x 3 + x 2 x ) dx (b) ∫ 3 1 (5 + x 2 x 2 ) dx (c) ∫ 5 1 ((2x + 3)(x – 2) x 4 ) dx (d) ∫ 4 3 (3x – 4)2 dx (e) ∫ –1 –3 3 (5 – 3x)3 dx (f) ∫ 0 – 2 2 ! 3 – 2x dx